La frequenza è naturale
Stasera mi son detto: aspetta un po' che mi ripasso come si usano i programmi degli elementi finiti. Aspetta va che mi guardo come faccio ad "unire" solidi con caratteristiche diverse in una simulazione.
Che oggetto mi creo per studiarmi un po' l'uso di questi programmini?
Uno sci fat!
Me lo disegno con misure realistiche e poi ci applico una struttura sandwich rozza e vedo come si comportano.
Ho disegnato uno sci composto da 4 (quattro) strati di materiale diverso aventi la stessa forma.
La forma degli sci è segnata nello schizzo sotto.
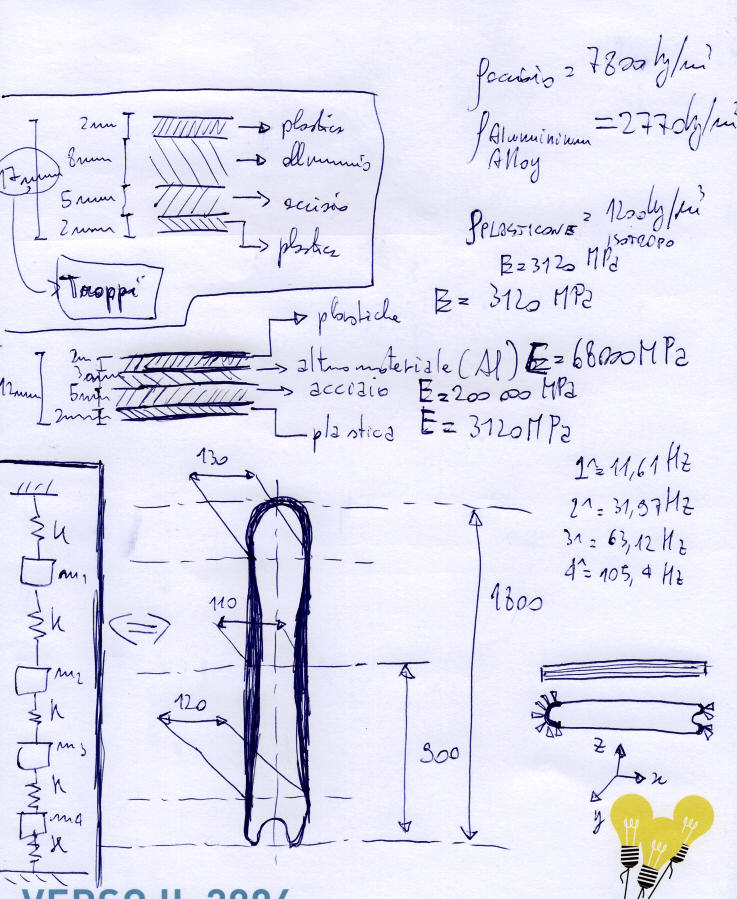
Caratteristiche Geometriche:
- larghezza centrale: 110 mm
- larghezza spatola: 130 mm
- larghezza coda: 120 mm.
Poi ho creato delle circonferenze tangenti a tre entità ed ho generato il profilo dello sci senza discontinuità.
Ho creato lo sci sovrapponendo 4 strati:
- soletta di materiale "tipo plastica" di 2mm;
- interno di 5mm materiale acciaio;
- altro strato di alluminio lega spessore 3mm;
- ricoprimento di plasticone da 2mm;
Ecco uno schema dei quattro strati. Ho fatto gli sci a coda di rondine D
D

Del materiale per queste anilisi conta il comportamento nelle diverse direzioni di sollecitazione ed io ho messo tutti materiali isotropi.
Il legno per esempio non è isotropo perchè resiste di più, per capirci, se lo tiro per lungo che non se lo tiro per una direzione ortogonale alle fibre.
Allora:
- plasticone: densità: 1220 kmg/m3; E: 3129 MPa;
- acciaio: densità 7800 kg/m3; E= 200000 MPa;
- lega alluminio: densità: 2770 kg/m3; E= 68000 MPa;
Opereremo solo in campo elastico; cioè, i nostri materiali supponiamo non si snervino e si deformino di una quantità proporzionale a quanta sollecitazione applichiamo su di essi.
Che cosa andiamo a calcolare?
Immaginate di avere in mano una corda elastica e ad una estremità di avere un sasso.
Voi volete allungare il più possibile la corda. Se voi iniziate a farla andare su e giù con una certa frequenza "esatta" vedete che la corda si allunga sempre di più. Se invece la sollecitate con una frequenza maggiore o minore il sassolino si sposta di meno.
Prendiamo una lunga bacchetta di ferro. Appoggiamola alle due estremità.
La vogliamo rompere facendola andare su e giù applicandoci la forza nel centro.
Viene istintivo applicarci la nostra forza, per esempio verso il basso ogni tot tempo, ovvero con una certa frequenza, giusto?
Ecco queste sono le frequenze naturali.
Ci sono per tutte le cose.
Il grosso problema è che se un oggetto viene sollecitato con una frequenza simile alla sua frequenza naturale questo "va in crisi"; uno paio di sci diventa instabile; i finestrini del bus vibrano il ponte cade.
La frequenza naturale di una cosa meccanica è data dal rapporto tra una rigidezza ed di una massa.
Ecco con il pc noi divideremo in tanti pezzettini i 4 strati degli sci, diremo al programma di unire questi pezzettini dove le facce degli strati combaciano e diciamo al pc: calcolaci la frequenza naturale dello sci.
Altra osservazione: la barretta di ferro di prima appoggiata alle estremità, abbiamo visto avere una sua frequenza naturale; se noi la incastrassimo completamente ad usa estremità ed iniziassimo a sollecitarla sull'altra la frequenza naturale trovata sarebbe diversa.
La frequenza naturale dipende da come vincoliamo l'oggetto.
Siamo pronti.
Suddividiamo gli sci in tanti elementini.
Più alto è il loro numero maggiore è l'accuratezza della simulazione ma maggiore è il carico richiesto al pc.
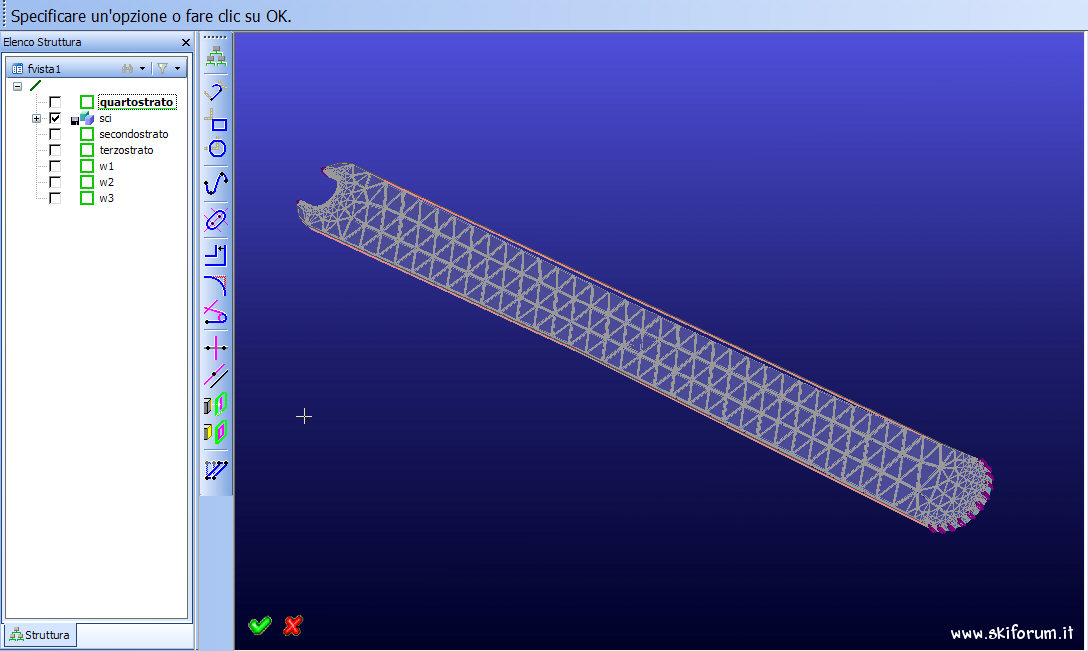
Meglio infittire la rete vicino ad elementi critici.
Così ho vincolato la coda.

Così ho vincolato la spatola: ho bloccato la traslazione in qualsiasi direzione dei nodi degli elementi concorrenti in quelle superficie.

Ed ecco la prima frequenza naturale, essa vale 11,61Hz. Se noi sollecitiamo gli sci con una forza che varia 11,61 volte in un secondo lo sci "entra in crisi". Supponiamo di viaggiare a 10m/s e di trovare un terreno con circa 11 cunette... Ecco, ci ritroveremo uno sci molto instabile, che balla tutto.
Prendete con le pinze le mie affermazioni!
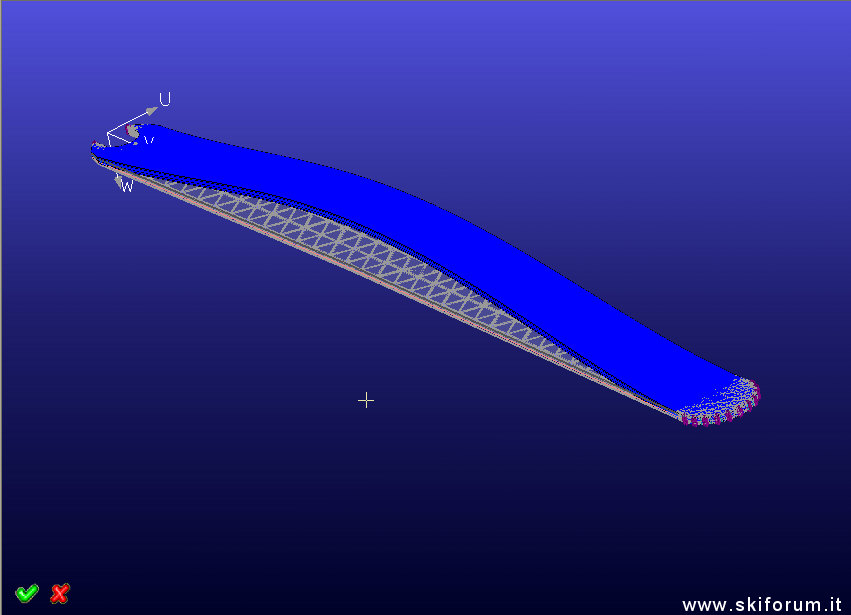
Questa è la seconda frequenza naturale: 31.97Hz.
Se noi lo stesso sci lo sollecitiamo con una forza con questa frequenza esso si metterà a muoversi con la forma in figura.

Terza frequenza naturale: 63,12 Hz.
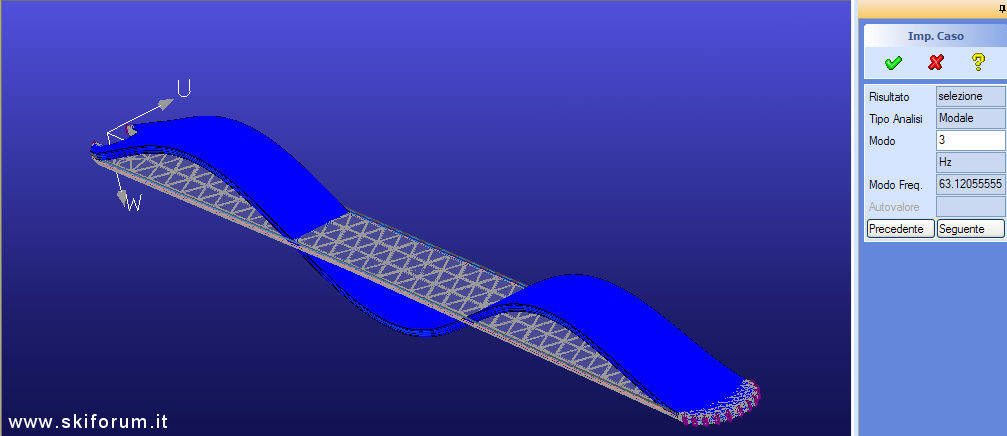
Quarta: 105,4 Hz.

Più avanti ci saranno freuquenze che faranno vibra lo sci lungo direzioni diverse, per esempio lo faranno torcere.
Prendete le cose lette come un gioco. Avevo un po' di tempo, mi era saltata la corsetta e dovevo ripassl'uso di questi programmi.
Resta il fatto che nonostante abbia usato 5 mm di acciaio che è una assunzione non troppo realistica, e nonostante le altre assunzione fatte "alla caxxo" il risultato di 11Hz mette in guardia!
Raggiungere frequenze di forzanti sull'ordine dei 20-25 Hz secondo me sciando ad una certa velocità non è impossibile. E' necessario quindi progettare lo sci, a mio avviso, con una frequenza prima per lo meno di 50 Hz e quest osignifica avere uno sci iperrigido e leggero che magari può andare contro le esigenze di poca rigidezza richieste per una sciata in fresca.
Quando si progetta uno sci è necessario avere bene in mente quale sarà il suo campo di utilizzo.
Vado via,
Buone cose,
Fabio
P. S.
Nello schizzo fatto a mano ci sono degli schemini utili per capire delle cose.
Stasera mi son detto: aspetta un po' che mi ripasso come si usano i programmi degli elementi finiti. Aspetta va che mi guardo come faccio ad "unire" solidi con caratteristiche diverse in una simulazione.
Che oggetto mi creo per studiarmi un po' l'uso di questi programmini?
Uno sci fat!
Me lo disegno con misure realistiche e poi ci applico una struttura sandwich rozza e vedo come si comportano.
Ho disegnato uno sci composto da 4 (quattro) strati di materiale diverso aventi la stessa forma.
La forma degli sci è segnata nello schizzo sotto.

Caratteristiche Geometriche:
- larghezza centrale: 110 mm
- larghezza spatola: 130 mm
- larghezza coda: 120 mm.
Poi ho creato delle circonferenze tangenti a tre entità ed ho generato il profilo dello sci senza discontinuità.
Ho creato lo sci sovrapponendo 4 strati:
- soletta di materiale "tipo plastica" di 2mm;
- interno di 5mm materiale acciaio;
- altro strato di alluminio lega spessore 3mm;
- ricoprimento di plasticone da 2mm;
Ecco uno schema dei quattro strati. Ho fatto gli sci a coda di rondine

Del materiale per queste anilisi conta il comportamento nelle diverse direzioni di sollecitazione ed io ho messo tutti materiali isotropi.
Il legno per esempio non è isotropo perchè resiste di più, per capirci, se lo tiro per lungo che non se lo tiro per una direzione ortogonale alle fibre.
Allora:
- plasticone: densità: 1220 kmg/m3; E: 3129 MPa;
- acciaio: densità 7800 kg/m3; E= 200000 MPa;
- lega alluminio: densità: 2770 kg/m3; E= 68000 MPa;
Opereremo solo in campo elastico; cioè, i nostri materiali supponiamo non si snervino e si deformino di una quantità proporzionale a quanta sollecitazione applichiamo su di essi.
Che cosa andiamo a calcolare?
Immaginate di avere in mano una corda elastica e ad una estremità di avere un sasso.
Voi volete allungare il più possibile la corda. Se voi iniziate a farla andare su e giù con una certa frequenza "esatta" vedete che la corda si allunga sempre di più. Se invece la sollecitate con una frequenza maggiore o minore il sassolino si sposta di meno.
Prendiamo una lunga bacchetta di ferro. Appoggiamola alle due estremità.
La vogliamo rompere facendola andare su e giù applicandoci la forza nel centro.
Viene istintivo applicarci la nostra forza, per esempio verso il basso ogni tot tempo, ovvero con una certa frequenza, giusto?
Ecco queste sono le frequenze naturali.
Ci sono per tutte le cose.
Il grosso problema è che se un oggetto viene sollecitato con una frequenza simile alla sua frequenza naturale questo "va in crisi"; uno paio di sci diventa instabile; i finestrini del bus vibrano il ponte cade.
La frequenza naturale di una cosa meccanica è data dal rapporto tra una rigidezza ed di una massa.
Ecco con il pc noi divideremo in tanti pezzettini i 4 strati degli sci, diremo al programma di unire questi pezzettini dove le facce degli strati combaciano e diciamo al pc: calcolaci la frequenza naturale dello sci.
Altra osservazione: la barretta di ferro di prima appoggiata alle estremità, abbiamo visto avere una sua frequenza naturale; se noi la incastrassimo completamente ad usa estremità ed iniziassimo a sollecitarla sull'altra la frequenza naturale trovata sarebbe diversa.
La frequenza naturale dipende da come vincoliamo l'oggetto.
Siamo pronti.
Suddividiamo gli sci in tanti elementini.
Più alto è il loro numero maggiore è l'accuratezza della simulazione ma maggiore è il carico richiesto al pc.

Meglio infittire la rete vicino ad elementi critici.
Così ho vincolato la coda.

Così ho vincolato la spatola: ho bloccato la traslazione in qualsiasi direzione dei nodi degli elementi concorrenti in quelle superficie.

Ed ecco la prima frequenza naturale, essa vale 11,61Hz. Se noi sollecitiamo gli sci con una forza che varia 11,61 volte in un secondo lo sci "entra in crisi". Supponiamo di viaggiare a 10m/s e di trovare un terreno con circa 11 cunette... Ecco, ci ritroveremo uno sci molto instabile, che balla tutto.
Prendete con le pinze le mie affermazioni!

Questa è la seconda frequenza naturale: 31.97Hz.
Se noi lo stesso sci lo sollecitiamo con una forza con questa frequenza esso si metterà a muoversi con la forma in figura.

Terza frequenza naturale: 63,12 Hz.

Quarta: 105,4 Hz.

Più avanti ci saranno freuquenze che faranno vibra lo sci lungo direzioni diverse, per esempio lo faranno torcere.
Prendete le cose lette come un gioco. Avevo un po' di tempo, mi era saltata la corsetta e dovevo ripassl'uso di questi programmi.
Resta il fatto che nonostante abbia usato 5 mm di acciaio che è una assunzione non troppo realistica, e nonostante le altre assunzione fatte "alla caxxo" il risultato di 11Hz mette in guardia!
Raggiungere frequenze di forzanti sull'ordine dei 20-25 Hz secondo me sciando ad una certa velocità non è impossibile. E' necessario quindi progettare lo sci, a mio avviso, con una frequenza prima per lo meno di 50 Hz e quest osignifica avere uno sci iperrigido e leggero che magari può andare contro le esigenze di poca rigidezza richieste per una sciata in fresca.
Quando si progetta uno sci è necessario avere bene in mente quale sarà il suo campo di utilizzo.
Vado via,
Buone cose,
Fabio
P. S.
Nello schizzo fatto a mano ci sono degli schemini utili per capire delle cose.
